Introduction to Federated Learning
The remarkable success of deep learning is mainly attributed to the availability of large amounts of data and computing power. With the advent of smart devices, abundant data is generated on a daily basis at different devices all over the world. We could leverage this data to train powerful deep-learning models. However, collecting this user-generated data for centralized processing is not practical because of communication and data privacy constraints. To address this concern, a new interest in developing distributed learning algorithms has emerged.
Federated learning (FL) is a popular setting in the distributed machine learning paradigm. In this setting, the training data is kept locally at the clients (edge devices) and a global shared model is learned by aggregating the locally computed updates through a coordinating central server. Note that Federated Learning exclusively focuses on data parallelism, in contrast to Split Learning which incorporates both data and model parallelism. Federated Averaging (FedAvg) is the first and most widely used FL algorithm.
Types of Federated Learning
The types of federated learning can be defined based on four different aspects namely data partitioning, resource constraints, and connectivity.
- Data Partitioning: Based on the data partitioning, federated learning can be divided into Horizontal FL and Vertical FL.
- Horizontal FL: Here all the clients have different sets of data samples but they have the same set of features. For example, let’s say we are looking at the Iris dataset. In the horizontal FL case, each client has a different subset of the dataset but all the clients have the same features i.e., petal length, petal width, sepal length, and sepal width. Horizontal FL is the most commonly used setup.
- Vertical FL: Here the clients may have the same data samples but different features i.e., each client has a different part of the data sample. Going back to the Iris dataset example, in the case of verticle FL (say with 2 clients), both the clients have the same or similar samples of flowers. But client-1 has petal length and petal width features, and client-2 has sepal length and sepal width features.
- Resource Constraint: Based on clients’ resource constraints say energy, power, and memory budget, Federated Learning can be divided into Cross-Silo and Cross-Device FL.
- Cross-Silo FL: Here the clients have massive computational power and memory. For example, a group of hospitals or government institutions collaborate to learn a model in a distributed setup.
- Cross-Device FL: Here the clients have limited resources. For example - mobile devices, drones, etc.
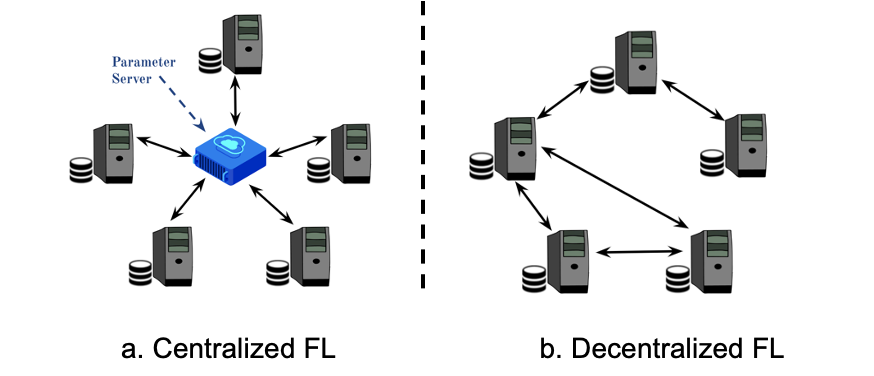
- Connectivity: Based on connectivity Federated Learning can be divided into Centralized FL and Decentralized FL.
- Centralized FL: In this setup, we have a central server that acts as an aggregator or a master, and all the clients are connected to the server. The clients send the local model updates to the server which then aggregates the information collected from all the clients and sends the updated model back to clients.
- Decentralized FL: In this setup, the clients are connected in a peer-to-peer manner getting rid of the central server. The information spreads across the clients like gossip i.e., each client communicates information to its neighbors and they send it to their neighbors and so on.
In all these cases, we assumed that models (ANNs) and data distributions are homogeneous. We can introduce heterogeneity in the system by having (a) different model architectures on different clients (eg: some clients have ResNet and some have MobileNet) or (b) different data distributions across clients (eg: some clients have more cats than tress and some have more trees than cats).
Federated Averaging (FedAvg):
FedAvg Algorithm is developed for a centralized federated learning setup with horizontal data partitioning and the data is Independent and Identically Distributed (IID). Let’s consider an FL setup with K clients connected to a server with no access to clients’ data and each of these clients contains an overlapping subset of a dataset (eg: CIFAR-10). Now, we want to train a model (eg: ResNet-20) on the entire dataset without directly sharing the data. To achieve this, we use the FedAvg algorithm. The following are the hyperparameters for FedAvg: B is the local batch size on each client, E is the number of local epochs between two consecutive communication rounds, p is the number of clients participating in each communication round, $n_k$ is the total number of iterations in E epochs for a given client $k$, the participation rate is $\frac{p}{K}$, learning rate $\eta$. The model parameters on all clients are initialized to the same values. We denote the model parameters at iteration $t$ on client $k$ by $x_k^t$ and on the server by $x^t$, $D_k$ is the data partition on client $k$. FedAvg algorithm executes as follows:
Server Executes
- initialize $x^0$
- for each communication round $t=1,2,…,T$ do
- Pick $S_t$ - a random set of p clients
- for each client $k \in S_t$ in parallel do
- $x^{t+1}_k$ = ClientUpdate($k$, $x^t$)
- $m^t = \sum_{k \in S_t} n_k$
- $x^{t+1} = \sum_{k \in S_t} \frac{n_k}{m^t} x^{t+1}_k$
ClientUpdate(k,x)
- Split $D_k$ into batches of size B and set $x_k = x$
- for each local epoch $i=1,2,…,E$ do
- for each batch $b$ do
- $x_k = x_k - \eta \nabla L(x_k,b)$
- return $x_k$ to server
At each communication round, the server randomly selects $p$ clients and sends them the most recent version of the model parameters. The clients, after receiving the model, run SGD locally for $E$ epochs and send the updated model parameters back to the server. Now, the server aggregates the information received from clients by updating the model parameters with the average of parameters received from each client. Note that the server computes the weighted average of the parameters received from the client where the weight for each client depends on $n_k$ i.e., the number of iterations (or updates) it performed in the current round.