Centralized federated learning setup requires frequent communication with the server which becomes a potential bottleneck. The server is usually connected to hundreds of clients and hence requires a very high network bandwidth reducing the communication speed. The server in such setups is a single point of failure. This has motivated the advancements in decentralized machine learning. Note that, in this post, the term federated learning implies centralized federated learning and decentralized learning implies decentralized federated learning.

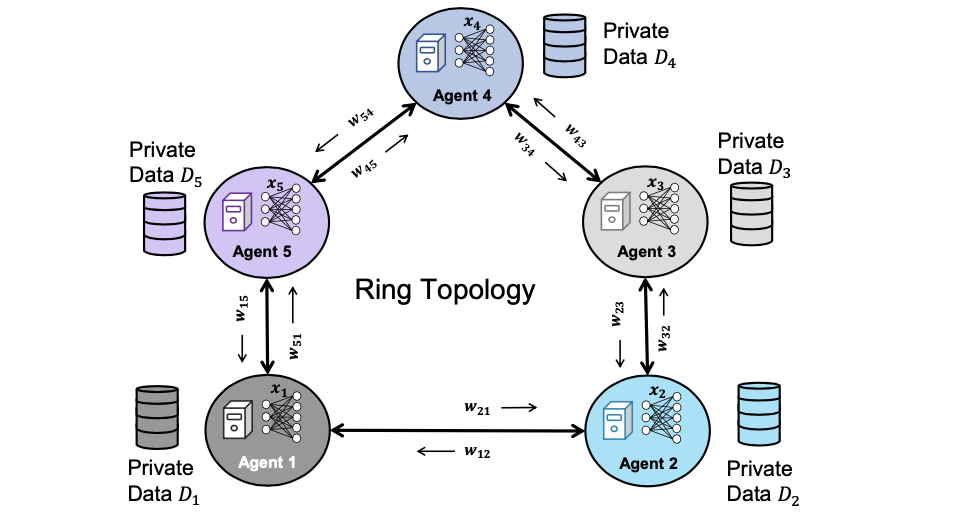
Decentralized learning is a branch of distributed learning that focuses on learning from data distributed across multiple agents/clients. Unlike federated learning, these algorithms assume that the agents are connected peer-to-peer without a central server. There are five main components of the decentralized learning setup:

  1. The agents that collaboratively learn task. The total number of agents is denoted by $n$.
  2. A sparse graph topology (G) that connects the agents with adjacency matrix $W$.
  3. Locally available data ($D_i$) on each agent $i$.
  4. A copy of model ($x_i$) on each agent $i$.
  5. Communication of model weights or gradients among neighboring agents.

The adjacency matrix $W$ of the graph is also known as the mixing matrix, weight matrix, or connectivity matrix.

Decentralized learning setup with 5 agents connected in a ring topology

Figure 1: Decentralized learning setup with 5 agents connected in a ring topology.


The main goal of decentralized machine learning is to learn a global model using the knowledge extracted from the locally generated and stored data samples across $n$ agents while maintaining privacy constraints. In particular, we solve the optimization problem of minimizing global loss function $f(x)$ distributed across n agents as given by the below equation. Note that $F_i$ is a local loss function (for example, cross-entropy loss $L_{ce}$) defined in terms of the data sampled ($d_i$) from the local dataset $D_i$ at agent $i$ with model parameters $x_i$.

$\min \limits_{x \in \mathbb{R}^d} f(x) = \frac{1}{n} \sum \limits_{i=1}^n f_i(x)$ where $f_i(x) = \mathbb{E}_{d_i \in D_i}[F_i(x; d_i)]$

This is typically achieved by combining stochastic gradient descent with global consensus-based gossip averaging. In particular, most of the decentralized algorithms have two components:

  1. Stochastic Gradient Descent (SGD): Each node uses its local data to update its copy of the model.
  2. Gossip Averaging: Each node aggregates the information received from its neighbors and uses it to update its model.

The first and most widely used decentralized algorithm is Decentralized Parallel Stochastic Gradient Descent (D-PSGD). Research has shown that decentralized learning algorithms can perform comparable to centralized algorithms on benchmark datasets under certain constraints. An in-depth explanation of D-PSGD can be found in a later blog.

<
Previous Post
Introduction to Federated Learning
>
Next Post
Gossip Averaging